The Mystery of Binary Numbers
|
You may remember learning in school long ago that our decimal number system is actually shorthand for an equation (though your teacher probably didn't used those words!). For example, (100) x 5 + (10) x 3 + (1) x 4 = 500 + 30 + 4 = 534 Each number in the final answer represents something more than just a single digit. For example, the 5 represents 500. |
You Are Here: |
|
|
|
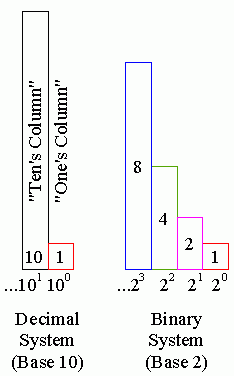
Our numbering system is based on the number 10, which is why it is called the decimal system (since deci- means ten). It means that we can display one of ten different values in each digit (0 through 9). But in computers, we use a number system based on the number 2 because we can only display two possible values in each digit (0 or 1, Off or On). We call this system a binary system (since bi- means two). The illustration at right shows a diagram comparing the decimal system to the binary system. Each digit is displayed as another column of blocks. Each column is the base raised to an exponent power. For that reason, these systems are also referred to as Base-10 and Base-2 number systems, respectively. To find the next larger digit of the decimal system in Figure 12, just increase the exponent from 102 = 100 to 103 = 1000. Doing the same thing for the binary system, the next digit would be 24 = 16. Let's do an example. |
 |
|
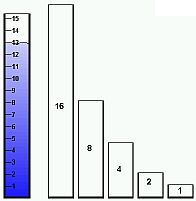
Example 1: What is the binary number for decimal 13? Solution 1: Imagine that instead of using blocks or digits, you are using beakers of water. Let's reword the problem in a new way: "You have a beaker with 13 ounces of water in it, and you need to pour it all out into several other beakers. You have an empty 16, 8, 4, 2, and 1-ounce beaker. Each beaker you fill must be filled completely (remember we can only have empty (0) or full (1) in binary). Which beakers will be filled?" The easiest way to find the binary equivalent to a decimal number is to start with the biggest possible "beaker" (i.e. 16, 8, etc.) and work your way down: |
|
|
We have 13 ounces. Can we fill the 16-ounce beaker completely? No.
We still have 13 ounces left.
|
 |
|
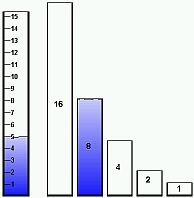
Can we fill the 8-ounce beaker? Yes. We have 5 ounces left (13 – 8 = 5). |
 |
|
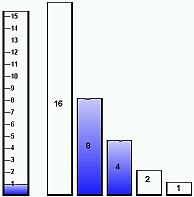
Can we fill the 4-ounce beaker? Yes. We have 1 ounce left (13 – 8 – 4 = 1). |
 |
|
Can we fill the 2-ounce beaker? No. We still have 1 ounce left. |
 |
|
Can we fill the 1-ounce beaker? Yes. (If you have any left, you need to try again). |
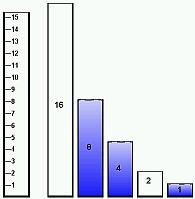 |
| Listing our answers in order from greatest to least, we have: No, Yes, Yes, No, Yes | |
|
In binary, that is: 0 1 1 0 1 Thus, decimal 13 equals binary 01101. |
|
When writing binary numbers, they are usually written in sets of 4, 8, 16, or 32 digits (called 4-, 8-, 16-, and 32-bit format). The 5-bit answer above is fine, but it is better to put it in either 4- or 8-bit format like this:
4-bit format: 1101 (this is acceptable as long as all digits to the left of the fourth digit would be zero)
8-bit format: 00001101 (this is acceptable as long as all digits to the left of the eighth digit would be zero)
Note that the extra zeros are all added to the left side. This would be like saying 163 is the same as 00163. We don't write decimal whole numbers like that, but it is acceptable and common in the binary system.
Example 2:
Find the decimal number for binary 00011001.
Solution 2:
Converting back to the decimal system from the binary system is a bit easier. You're just taking all the binary "beakers" and pouring them back into a graduated decimal "beaker." Take the binary digits and multiply them out like the "elementary school equation" referred to at the beginning:
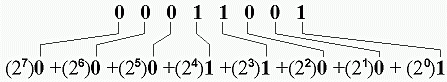
Multiplying out the exponents:
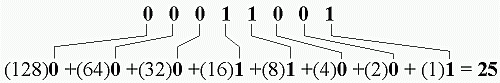
| A Point to Ponder - If you ever wondered why computer parts like Random Access Memory (called RAM) always come in strange sizes (like 64, 256, or 512 Megabytes), the reason is that they are designed around base-2 numbers! For example, 26=64, 28=256, and 29=512. Now you know! |